Search and Planning in games

Definitions

1. Initial State:- Initial board position.
2. Terminal Test:- Determines whether the game is over.
3. Terminal State:- State where the game has ended.
4. Utility Function:- Numeric value given to terminal states. For example, in tic-tac-toe, win = +1, loss = -1 and draw = 0.
5. Ply:- Turn of a player.
6. Game Tree:- Initial states and the possible states obtained after legal moves whose depth is measured in terms of plies.
7. Optimal strategy:- A strategy that can give outcomes atleast as good as any other strategy when playing against an unerring player.

Minimax algorithm

1. It returns the minimax decision from the current state, i.e, it optimizes the "worst case outcome" for MAX.
2. MINIMAX_VALUES for a node is defined as the minimum of the utility functions of the successors if the ply is of the MIN player and maximum value of the utility functions of the successor if the ply is of the MAX player.
3. The MINIMAX_VALUES for all of the nodes are calculated and the node with highest value is chosen as the best move.

Minimax Theorem and Game Theory

In Game theory, Minimax theorem deals with finding the best move in a particular situation. In other words, the resulting outcome of a game can be predicted if all players play the best, most rational strategy.

For the sake of simplicity, let us consider 2 player zero sum games. In a zero sum game, the total value of the game stays the same or goes down e.g. chess, tic-tac-toe, Checkers etc. Coming up with an ideal strategy for a game such as tic-tac-toe is a fairly easy task.

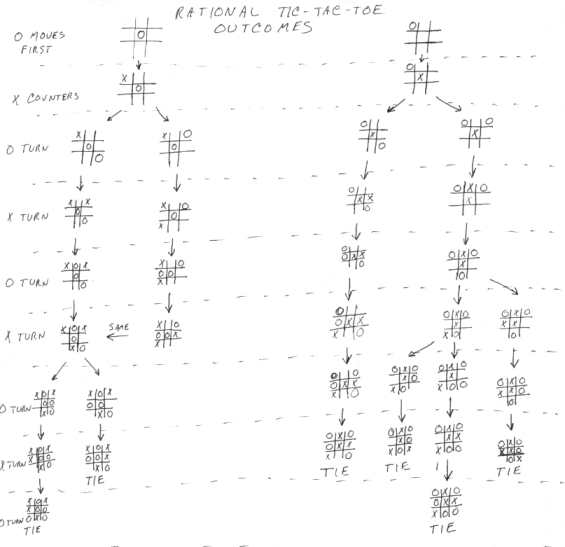
 Image source : http://members.cox.net/mathmistakes/game_theory.htm

However, for a game like chess which is highly complex, defining an ideal strategy is a complicated task.

Chess Search Techniques

Chess has been by far, the most researched board game. The development of a chess playing machine started in 1950 when Claude Shannon predicted that there could be two possible search strategies in chess-

Type A- A brute force based strategy where every position possible would be analysed for fixed number of plies using the minimax algorithm based on the evaluation function of a given chess position which is a heuristic approximation of the worth of different chess pieces and their relative positions. However, this would waste a lot of time examining the really bad moves which would normally be ignored. Also, it would ignore the quiet stages (quiescence) of a game where the evaluation function does not change by much and adapting to it would waste more time.

Type B- This would encompass the following improvements-

1.      Implement a quiescence search- If a non quiescent state is to be evaluated, the game state would be expanded until a quiescent state is reached and the evaluation function for that would be used.

2.       Removing the Horizon Effect- Rather than searching all the positions to a similar depth, search only the interesting ones to a greater depth.

Type B, to a great extent mimics how a chess grandmaster contemplates a move. The early chess programmes, most notably the Chess 4.0 abandoned Type B searching and were very successful during the 1970�s. Later, a selective part was included in these programmes based on quiescence searches, and extensions (extending interesting moves) and pruning (discarding bad moves). The Deep Blue Computer, developed by IBM, defeated World Champion Garry Kasparov in 1997. It could evaluate 200 million positions in a second and relied minimally on selection.

Alpha-Beta Pruning

1. It finds the correct minimax decision without looking at the each and every node by pruning certain subtrees.
2. The subtrees can be pruned by just keeping track of the two parameters.
   = Highest value along the path of MAX.
   = Lowest value along the path of MIN.
   

Case of sub-optimal players

References