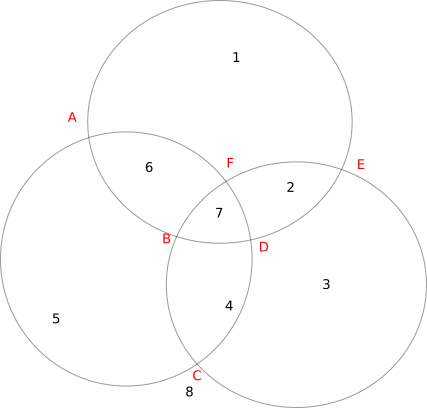
Venn diagrams offer a pictorial view of the relationships between sets. We often see Venn diagrams using circles, which depict the relationships that can occur between 2 sets or 3 sets. For example, the following Venn diagram illustrates the relationships between 3 sets.
Can we draw a Venn diagram depicting all the relationships that can exist between 4 sets using circles?
The Euler characteristic of a geometric figure is defined as V-E+F, where V is the number of vertices, E the number of edges, and F the number of faces (regions).
For any planar figure, the Euler characteristic is 2. (Try it for a square: V=4,E=4,F=2 giving V-E+F=2, and a triangle: V=3,E=3,F=2, giving V-E+F=2 or the following figure with V=4,E=5,F=3.)
Any Venn diagram is a planar figure, so V-E+F will be 2. We can verify that from Figure 1, where V=6,E=12,F=8, yielding V-E+F=2.
The crucial point is this: Two distinct circles can intersect only in exactly 0, 1 or 2 points. For purposes of Venn diagrams, we need to consider only pairs of circles which intersect each other in exactly 2 points.
To simplify the number of cases, let us assume that each distinct pair of circles corresponds to a distinct pair of intersection points. [footnote]
Let us try to introduce a fourth circle into the figure. The fourth circle which is being introduced brings 6 more vertices. Thus V=12. Each vertex has degree 4. (figure).
It is an easily established fact that for any graph, the sum of the degrees of vertices is twice the number of edges. Hence E=24. But since we need a planar figure, we must have F = 2-V+E = 2-12+24 = 14.Thus it is not possibe to represent 16 regions using Venn diagrams consisting of 4 circles.
(Ellipses, Ovals, Triangles etc. can be used to represent relationships between 4 sets.)The number of pairs formed by n circles is n(n-1)/2. The number of vertices in the intersection figure is therefore n(n-1), if the Venn diagram exists as a planar figure. The number of edges is 2n(n-1). For the Venn diagram to exist, we must have
n(n-1) - 2n(n-1) + 2^n = 2.
Since 2n is asymptotically greater than n(n-1), the only two values of n for which the equation can be satisfied are n=2 and n=3.
Once, in a discussion, I and my friend wondered whether John Venn deserved undying fame for such a trivial concept. In the light of the above discussion, it is easier to appreciate Venn's contribution - he gave a geometric scheme to depict relationships between n sets for arbitrary n (!!) Of course, he had to use a recursive scheme using weird shapes.
FEEDBACK: Not convinced by the argument? Email me improvements/corrrections at satyadev@cse.iitk.ac.in.