CS365 Artificial Intelligence

Homework 1: Computer Vision

Submission: online as a HTML file (see below).

A. [LINE LABELLING] Prove that under the trihedral assumption, 
   only 3 Types of arrow junction are possible. 

B. [STEREO IMAGING] 
    i. Stereo system for terrain mapping [Problem 24.6 in book]
    Note: to evaluate dZ, you need to use the formulation in terms
	of delta-theta (p.906 bottom) which shows it growing inversely as
	Z-squared.  
    ii.  How does this expression correlate with the expression given in
        class, where we differentiated the pinhole equation to obtain an
	expression for du that was inversely proportional to Z.  

C. [CAMERA TRANSFORMATIONS]

Consider a camera mounted on a window of the CSE building facing outwards
s.t. the optical center is 4 m high and 2m of to the right of the gate, and
its optical axis is looking out (i.e. as if standing with your back to the
building).  

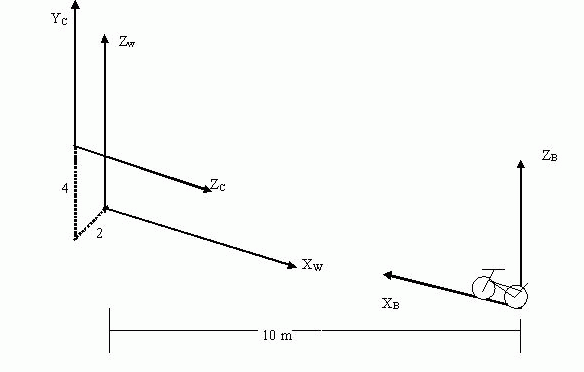
A bicycle approaching the building is currently 10m and facing the gate
moving parallel to the camera -Z axis at 2 m/sec.  The bicycle local frame B
is fixed at the point where its rear-wheel meets the ground (-2, -4, 10) in
Camera coordinates [or (2,-4,10) if we take X axis as a right-handed frame]
and its x-axis faces forward. 
Note: A solution with either of these coordinates will get full marks.
In this frame, the right tip of its handlebar (when it is going straight) 
is at P = (1.5,-0.2,0.8).

a. Determine the u,v for the image p of this point P for a pinhole camera
   with f = 0.1m, and pixel size 0.1mm x 0.1mm.  Assume image size is 1K x
   1K (gives a ~ 45 degree field of view) and that (u,v) is measured from 
   an origin at the bottom left of the image. Assume the principal point of 
   the image to be at the exact center, and that there is no skew, and that 
   pixels are square. The image plane can be taken in front of the pinhole 
   as presently adopted in class, but you may also put it behind - which 
   will just change the sign. 

b. Determine the velocity of the point p, the image of P.  As the bicycle
   approaches the building will your computed velocity increase or decrease? 

Submission

The solution is due on Jan 27 2PM at http://home.iitk.ac.in/~userid/cs365/hw1/index.html You should create a simple html file, images if needed, may be scanned. Please note that the deadline has to be strictly followed as the Solution will be discussed in the class.