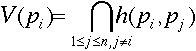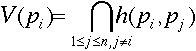VORONOI  DIAGRAMS

Submitted By: Kshitij Judah

Roll No: 98178

Course No: CS698R

Course Name: Robot Motion Planning

Instructor: Dr. Amitabh Mukherjee

DEFINITION:-

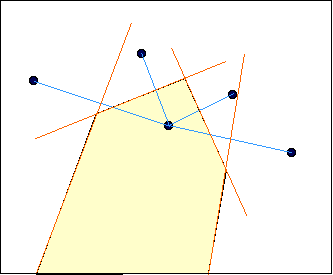
•  The voronoi diagram is a partition of plane into cells, directed by a set of points P = {P1,P2,......Pn} such that for  each cell corresponding  to point Pi, the points q in that cell  are nearer  to Pi  than any other point P.            dist(q,Pi) < dist(q,Pj);  Pi, Pj are elements of set P and i and j are not equal.
• If we partition the plane into half planes, each half plane being constructed with the bisector of the line between Pi and Pj , then we can form the voronoi diagram as the intersection of the half planes.

• Hence in a way, voronoi diagram represent the region of influence around each of the given set of points.        

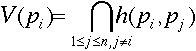
 PROPERTIES (WITHOUT PROOFS):-

• If the points P are collinear, the voronoi diagram consists of n-1 parallel lines forming n cells.
• If the points P are not collinear, the edges of the voronoi diagram are segments, or half lines( which may terminate at useful border).
• The number of vertices in a voronoi diagram of a set of n points is at most 2n-5 and the number of edges are at most 3n-6.
• Voronoi cells or voronoi partitions are convex.
• The voronoi cell of Pi is unbounded if Pi lies on the convex hull of P.
• "Largest Empty Circle of q wrt P" is the largest circle whose center is q and which contains no point of P in its interior. A point q is a vertext of a voronoi diagram if its largest empty circle has three or more points of P on its circumference. This circle is the circumcircle of the corresponding Delaunay Triangle.
• The bisector between Pi and Pj defines an edge of the voronoi diagram of P iff there is a point q in the plane such that its largest empty circle contains both Pi and Pj on its circumference and no other member of P.

• The dual of the voronoi diagram is the Delaunay Triangulation.         

                                                                            Delaunay Triangulation                                                                     

APPLICATIONS OF VORONOI DIAGRAMS:-

 There are many fields where voronoi diagrams are used (although often not by that name). Some of these are as follows:-

• ASTRONOMY:-  Identify clusters of stars and clusters of galaxies.
• GEOGRAPHY:-   Analyzing patterns of urban settlements.
• METALLURGY:-  Modeling "grain growth" in metal films.
• BIOLOGY, ECOLOGY, FORESTRY:-  Model and analyze plant competition (" Area potentially available to a tree", "plant polygons").
• ROBOTICS:-  Path planning in presence of obstacles.

Apart from above fields, voronoi diagrams are used in computer science also especially in a branch of computer science called computational geometry. Below are some problems of computational geometry where voronoi diagrams are used:-

• Knuth's post office problem:-  Given a set of locations for post offices, how do you determine the closest post office to a given house?
• Closest pair problem:-  Given a set of points, which two are closest together?
• All nearest neighbors problem:-  Given a set of points, find each point's nearest neighbor.
• Euclidean minimum spanning tree:-  Given a graph, find out a tree which includes all vertices of the given graph and also it should be the minimum weight tree, weight being measured as the Euclidean distance between the two vertices forming the edge.

ALGORITHMS FOR CONSTRUCTING VORONOI DIAGRAMS:-

There are many algorithms for constructing the voronoi diagrams. Some of them are as follows:-

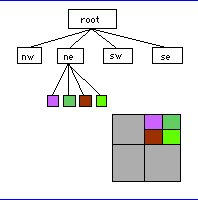
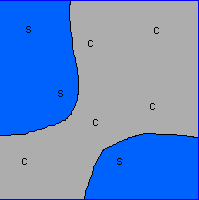
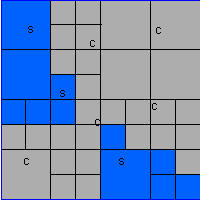
• AN IMAGE SPACE ALGORITHM:- 
• Operates in display coordinates, develops the voronoi diagram on the display.
• Difficult to construct polygons, construct "regions".
• Easy to construct regions formed by adjacent voronoi cells with same characteristics.
• It is a quadtree algorithm.
• Recursively subdivide the plane into quadrangles until each quadrangle contains only points closer to Pi than to any other Pj.

• HALF PLANE ALGORITHMS:-
• Construct the perpendicular bisectors.
• For a given Pi, begin with the nearest Pj and the perpendicular bisector of this Pi-Pj.
• "Walk around the voronoi diagram, looking for the next intersection with another bisector or with the border.
• Easy to construct polygons, but somewhat more difficult to merge adjacent voronoi polygons with same characteristics.

• DIVIDE AND CONQUER ALGORITHM:-
• Divide the input points into two half sets Vl and Vr based on their geometric positions.
• Recursively create voronoi diagrams VDl and VDr for those two sets respectively.
• Merge VDl and VDr to create voronoi diagram VD for the whole set.
• Key operation is the O(n) merge step.
• Merge step builds a bisector polyline that separates the points( also called sites ) of Vl and Vr and it prunes away the defunct geometry from VDl and VDr.    

• INCREMENTAL ALGORITHMS:-
• Inserts the points one at a time into the diagram.
• When a new point comes, we figure out which of the existing voronoi cells contains the new point.
• Then "walk around" the boundary of the new point's voronoi cell (also called voronoi region or voronoi partition)    inserting new points into the diagram.
• Finally delete all the old edges sticking into the new region.
• Worst case running time is O(n^2).
• It has been proved that if the points are inserted in some random order, then running time reduces to O(n*logn).   

• FORTUNE'S ALGORITHM:-
• It is a sweep line algorithm.
• The intersection of two cones whose axes are vertical is a parabola.
• If the cones have their apex at the points in P, then these parabolae lie in vertical planes and their projections onto x-y plane is a straight line.
• If the field of cones opening towards the +z axis is viewed from below and the cones are opaque, the view gives the voronoi diagram .
• In fortune's algorithm, a sweep line moves across the x-y plane, and a sweep plane, inclined at an angle of 45 degrees to the x-y plane and passing through the sweep line, sweeps through a field of cones. As it sweeps, it detects voronoi vertices and edges.
• Worst case running time is O(n*lgn).      

USE OF VORONOI DIAGRAMS IN ROBOTICS:-

• A path planning technique known as the retraction approach uses voronoi diagram for path planning.
• It consists of retracting Cfree onto its voronoi diagram where Cfree means set of all free configurations.
• This diagram has the property of maximizing the clearance between the robot and the obstacles.

FEW DEFINITIONS:-

• Let X be a topological space and Y be a subset of X. A surjective map r X->Y is called a retraction from X to Y if and only if it is continues and its restriction to Y is the identity map. 

• Let B denote the boundary of Cfree. For any q which is element of Cfree let:    

                                                      clearance (q) = min || q-p ||; where p is element of B,

           where || q-p || is the Euclidean distance between q and p.

• Let  near (q) = {p | || q-p ||  =   clearance (q) } where p is element of B.      

• The voronoi diagram of Cfree  is the set:      

                                              V or (Cfree) = (q | card (near (q)) > 1 } where q is element of Cfree   

           where card (E) denotes the cardinality of the set E.

• V or (Cfree) consists of finite collection of straight and parabolic curve segments called arcs.    

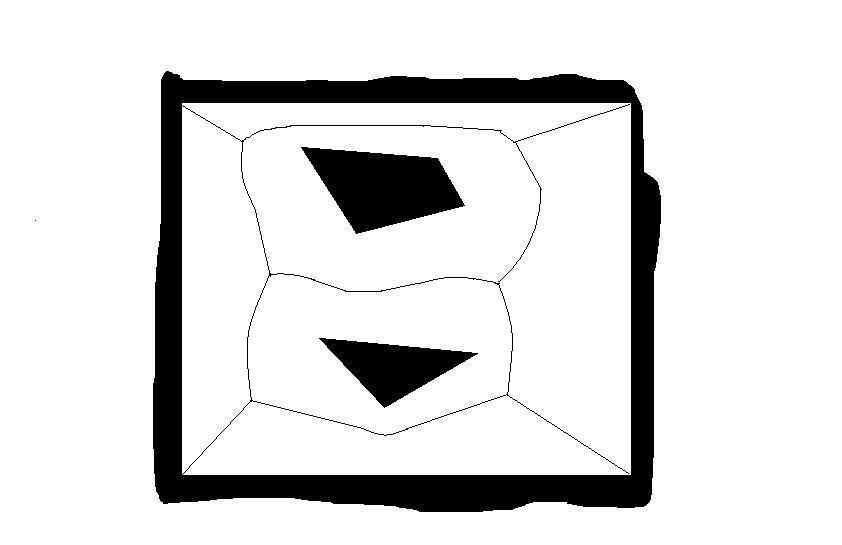
                                                                                voronoi diagram of Cfree   

• Retraction approach proceed as follows:-
• Compute the voronoi diagram V or (Cfree).
• Compute the points r(qinit) and r(qgoal) and identify the arcs of V or (Cfree) containing these two points.
• Search V or (Cfree) for a sequence of arcs A1, A2, .........., An such that r(qinit) is element of A1, r(qgoal) is element of An and for all i from 1 to n-1, Ai and Ai+1 share an endpoint. 
• If successful, return r(qinit), r(qgoal) and the sequence of arcs connecting them, else return failure.     
• Overall time complexity of this algorithm is O(n*logn).
• Also applicable when c-obstacles are generalized polygons.     

• Other retraction methods have been been proposed to solve more involved instances of basic motion planning problem.
• One such method was proposed by O' Dunlaing, Sharir, and Yap which plans motion of a segment which plans motion of a segment ("ladder")  among polygonal obstacles.
• In this method, the three dimensional free space is first retracted onto a two dimensional variant of the voronoi diagram. In a second step, this diagram is itself retracted onto a network of one dimensional curves of Cfree.
• The whole computation takes O(n^2*log(n)*log(log(n))) time.
•  Many authors suggested using the voronoi diagram of the empty subset of a two dimensional workspace as a heuristic guideline to plan free paths for a robot that can both translate and rotate in a plane. (e.g. see [Takahashi and Schilling,  1989] ). 

• One issue in the above retraction approach is the calculation of the voronoi diagram of Cfree since obstacles are polygons and not discrete points. These polygons could be both convex and concave.
• To find the voronoi diagram for this collection of polygons, one can either compute the diagram exactly or use an approximation based on the simpler problem of computing the Voronoi diagram for a set of discrete points.
• In the latter case, we first approximate the boundaries of the polygonal obstacles with the large number of points that result from subdividing each side of the original polygon into small segments.
• Second, we compute the Voronoi diagram for this collection of approximating points.
• Once this complicated Voronoi diagram is constructed, we then eliminate those Voronoi edges which have one or both endpoints lying inside any of the obstacles. The remaining Voronoi edges form a good approximation of the generalized Voronoi diagram for the original obstacles in the map.

DELAUNAY TRIANGULATION:-

• It is dual of the voronoi diagram.
• It is constructed by drawing line segments between any two sites whose voronoi regions share an edge.
• Splits convex hull of the given set of points into triangles.

       PROPERTIES:-

• Each point is connected to its nearest neighbor by an edge in Delaunay Triangulation.
• It is a planar graph and hence by Euler's formula has at most 3n-6 edges and at most 2n-5 triangles. Here n is the number of points (sites) given.
• The empty Circle property: If you draw a circle passing through the vertices of any delaunay triangle, then no other sites will be inside that circle.
• It contains "fat" triangles, in the sense that minimum angle of any Delaunay triangle is as large as possible. If you write down a list of all angles in the Delaunay triangulation, in increasing order then do the same thing for any other triangulation, of the same set of points, the Delaunay list is guaranteed to be lexicographically smaller.