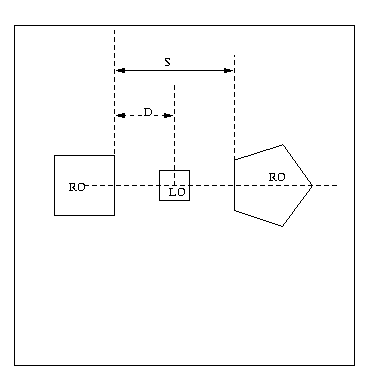
MULTIPLE ROs AND THEIR EFFECT ON THE POSITIONING OF THE LO
Here, we considered the problem of placing the LO between
2 ROs as the distance between them / their relative size varied.
In case of distance variation, the various
distances between the ROs considered were:
Case 1: 500 units
Case 2: 380 units
Case 3: 260 units
In the tests run, one RO was a square, and the other was
a pentagon, and their sizes were kept the same.
The size of the square LO was taken to be the same over the entire suite
of 3 tests.
In case of the relative size variation, the
different sizes of the pentagon that were considered were:
Case 1: 100 units
Case 2: 75 units
Case 3: 50 units
Case 4: 25 units
The size of the square RO was kept constant at 60 units and the size of the circular LO was also kept fixed over the entire suite of 4 tests.
The dependent variable was the position of the sweet spot.
To see the conclusion, click here
DISTANCE VARIATION
We start off with the assumption that the Y-Coordinate of the centre of the LO will not vary as the boundary changes. This can be concluded from our analysis of previous results e.g. shape effects of LO. Even for this suite of tests we have verified this independence but the analysis is not shown here for sake of conciseness.
Applying ANOVA to the X-Coordinates of the center of the LO, we get the following results:
|
MEAN |
MEAN |
MEAN |
F-RATIO |
|
244 |
189 |
137 |
238.171 |
The wide difference in the mean values of the X-Coordinates given above, and also the high value of the F-ratio suggest that the X-Coordinate of the center of the LO varies greatly with distance.

We now construct a table between D and S, where D and S are as defined above.
|
D |
184 |
129 |
77 |
|
S |
392 |
272 |
152 |
Linear regression was performed on the values
contained in the table given above, and D was calculated as a function
of S as:
D = k + 0.45*S
where k is a small constant.
From the above analysis we have concluded that when asked to place the LO between 2 ROs, a human subject places the LO almost exactly in the middle of the available space between the 2 ROs, along the line joining the centers of the 2 ROs
RELATIVE SIZE VARIATION
We start off with the assumption that the Y-Coordinate of the centre of the LO will not vary as the boundary changes. This can be concluded from our analysis of previous results e.g. shape effects of LO. Even for this suite of tests we have verified this independence but the analysis is not shown here for sake of conciseness.
Applying ANOVA to the X-Coordinates of the center of the LO, we get the following results:
|
MEAN |
MEAN |
MEAN |
MEAN |
F-RATIO |
|
282 |
290 |
313 |
312 |
7.8484 |
The wide difference in the mean values of the X-Coordinates given above, and also the high value of the F-ratio suggest that the X-Coordinate of the center of the LO varies greatly with distance.
We now construct a table between D and S, where D and S are as defined above.
|
D |
123 |
130 |
153 |
153 |
|
S |
260 |
280 |
300 |
320 |
Linear regression was performed on the values
contained in the table given above, and D was calculated as a function
of S as:
D = k + 0.56*S
where k is a small negative constant.
From the above analysis we have concluded that when
asked to place the LO between 2 ROs, a human subject places the LO almost
exactly in the middle of the available space between the 2 ROs, along the
line joining the centers of the 2 ROs
CONCLUSION
Thus, from the above analysis, we conclude that when asked to place a LO between 2 ROs, a human subject places the LO almost at the center of the space available between the 2 ROs, along the line joining their centres, and this placement does not depend appreciably either on the distance between the 2 ROs or on the relative sizes of the ROs.