Computer Aided Engineering Design ME 751/451 Jul-Nov 98 Mukerjee

 
Trajectory simulation for PUMA-560

Swaroop K Chalasani, 9810541
PAV Prasad ,98
Indian Institute of Technology - Kanpur : August 1998


 


Contents


Motivation

Importance of Simulation?
Today simulation is necessary from small videa-games to atomic explostion testing. As per the industry requirement- for efficient process planning, path planning of robots, analyzing the rate of production simulation is very essential. e.g In aeromodelling, construcing parts and then testing that part for feasible joperation is costly and moreover we may not converge to a good design. Before embarking on actual manufacturing, jone can generate the same part and aply the working conditons on the part generated through simulation. In FMS(Flexible Manufacturing Systems), study of robots in the owrk cell is done by simulation.Also , one cannot afford to stop a robot , which is on-line,like assembling and do the programming for the next task.The other way is to simulate the same commamnds in a simulator, and check the various possibilities. This is known as 'off-line programming'. As these simulators, which try to simulate robots are very costly, like 'DENEB', our work attempts to simulate the robot movements along a planned trajectory. 

Example

Imagine a package which consists of simulation of PUMA-560, in which one can specify a point and orientation can see the position and configuration of the manipulator in workspace. Similiraly, if another point with other orientation is specified, then a trajectory like cubic spline or straight line can be fitted between these two points and the robot is animated along this planned trajectoru. The summary of this whole process can be explained as follows: 
     INPUT:

                  Point-1   : { xi,yi,zi}, { O,A,T}  where 'O' is orientation ,'A' is altitude, 'T'                                             is tool angle.


 Point-2   : { xf,yf,zf},{O,A,T}

         Trajectory:cubic spline

                 configuration: Arm(left/right),elbow(up/down),wrist(flip/no-flip)

                 Time of travel:
   OUTPUT:
Set of interpolated joint angles and the display is the animation of robot through these joint angles. Our present work is able to give the joint angles of all the joints when cartesian coordinates and the euler angles are given.And also the cartesian point as well as the orientation when the joint angles are given.It is only possible to fit a cubic curve between the two points when simulation is to be carried out.Our problem obviously dont take care of the dynamic nature of the environment i.e. obstacle avoidance, collision detection etc. Also it is not possible to fit any curve in between the two points.

Past Work

Much work is going on around the world to simulate a comple workcell in which many co-operating robots navigates and manipulates along with the lines of assembly system. Eventually these packages were kept at exorbitant prices. Traditionally, universities used to make some simulations and for them PUMA series was a natural choice. In IITK also, this was carried as a Thesis Work by an M.Tech student. 

Assumptions

  • Initial and final velocities are assumed to be zero.
  • All the three axes at the end are concurrent for PUMA-560.

    • Sample Input and Expected Output

    The simulation consists of various CGI and GUI outputs which are listed as follows Direct Kinematics simulator: In this module the user specifies all the Joint angles (6), and he can get the the output of position of end-effector in cartesian system. If user anticipates to see what will be the configuration for the given angles, he can check on visual display; Apart from these the results were checked with PUMA-560. The input- output are as follows 
            INPUT:
                theta-1 = 21
                theta-2 = 24
                theta-3 = 50
                theta-4 = 104
                theta-5 = -78.7
                theta-6 = -199
        OUPUT:
                a)
                
                x = 729
                y = 383.7
                z = -38

                O ( orientation ) = 36
                A ( altitutde   ) = 9.7
                T ( Tooling     ) = -8.7

                ARM = -1 = LEFT
                ELBOW = 

                b)  GUI display

             (one can check the validation of this solution of PUMA)
             
INVERSE KINEMATICS:
        
        Inverse kinematic equations for gemetric solution of PUMA-560 were formed and
        algorithemized.  One can check the validity of inverse kinematic solution through
        this module.  The input for this module is of two forms
                
                INPUT-I:

                        x =  583.19 
                        y =  -400
                        z =  -348

                        
                        orientation matrix [n s a] ( 3X3)  obtained from direct kinematics
                        
                        [   nx sx ax
                            ny sy ay
                            nz sz az ]

                        For this case the results were exactly matching with those of
                        forward kinematics input;
                        
                INPUT-II:
                        
                        x = 140           theta-1 = 133
                        y = -410          theta-2 = -138 
                        z = 765           theta-3 = 132
                                     
                        O =   -35         theta-4 = 90
                        A =   -61         theta-5 = 28.2 
                        T =   145         theta-6 = -201.5  
                        For this case the results were not exactly matching;  There comes
                        error due to less unknowns, many equationss;  The error for position
                        is very low where as for orentation, its a bit high;

    METHODOLOGY



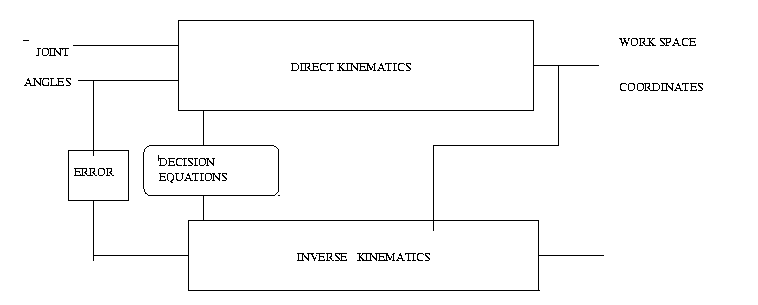
    There are two methods in which the kinematic analysis of a manipulator can be analysed:

    (1) direct kinematics and
    (2) inverse kinematics.

    In direct kinematics, Joint angles of each of the link is specified and depending on these joint angles the end effector is described in cartesian coordinates as well as orientation. In inverse kinematics, the cartesian coordinates as well as the orientation of the tool is given with respect to the global frame. From this data the joint angles are determined. Direct kinematics is easy to implement and the kinematic equations are straight forward.But the complexity is in determining the combination of joint angles which can reach the desired point in the cartesian space. Inverse kinematics are computationally difficult but user can comfortably specify the point where he want to move the manipulator in the work space. For direct kinematic analysis the equations are derived by using simple trigonometry but for inverse kinematic analysis there are three methods to do the computation:
    (1)PIEPERS SOLUTION

    (2)GEOMETRIC SOLUTION

    (3)ALGEBRAIC SOLUTION

    In our project we have implemented the Geometric solution.

    ANALYSIS:
    When inverse kinematics is applied eight possible set of solutions are possible-two for the arm, two for elbow and the three for the wristi.e. Arm(left/right),elbow(up/down), wrist(up/down).The combinations of these three gives the eight valied configurations of the manipulator in the work space.
    In employing the geometric solution, since the user also specifies the configuration of the manipulator(Arm,elbow,wrist) the number of the possible solutions are reduced with this specification..After specifing there are still two possible solutions-depending on the FLIP/NO-FLIP condition obtained from the calculations. The inverse kinematic equations for finding the joint angles is given in the book authored by LEE. The various arm configurations are entered as input as

    ARM = +1 RIGHT ARM
    -1 LEFT ARM
    ELBOW = +1 ABOVE ARM
    -1 BELOW ARM
    WRIST = +1 WRIST DOWN
    -1 WRIST UP

    In the direct kinematics analysis, the decision equations for obtaining the arm, elbow, wrist configurations are also given in book by K.S.FU.
    In the input the user specifies the cartesian coordinate and the orientation of the tool frame with respect to the world coordinate( while doing the inverse kinematics).And also the arm,wrist, elbow configurations.These values are substituted in the equations for finding the joint angles and the joint anglesd are found out. In direct kinematic analysis the user input the joint angles and the cartesian point as well as the orientation of the end effector is obtained( the end effector point is taken in middle of the fingers of the gripper).
    After finding the joint angles at two different positions , a cubic spline is interpolated between these two points to get the intermediate joint angles of the manipulator when it is made to follow this path.The interpolation can be done in two ways- TASK SPACE SCHEME and JOINT SPACE SCHEME. If the interpolation is done between the initial and final cartesian coordinatesand euler angles,then it is called TASK SPACE SCHEMES. And if the interpolation is done between the initial and final joint angles then it is called JOINT SPACE SCHEMES.
    In our present work we're doing joint space schemes because they are easy to implement andless computational whereas task space schemes are very difficult to implement.

    COMPUTER SIMULATION:

    A computer program is written to verify the validity of the inverse solution of the PUMA robot arm . The software initially inputs the data into the direct kinematic routine to obtain the arm matrix.These joint angles are also used to compute the decision equations to obtain the three arm configurations. These configurations together with the arm matrix T are fed into the inverse solution routine to obtain the joint angle solution which should agree to the joint angles fed into the direct kinematics routine previously. If only the inverse kinematic routine is carried out with the input then the results obtained have errors in the joint angles calculated and these errors are more prone in the orientation anglesi.e. the last three angles.The reason for this is the error in angle of first ,second angle and third angle gets added up and this error is reflected more in the orientation matrix from which we'll find the last three angles.The software required is developed using the following:

    (1)MATLAB: This is used for all the inverse ,direct and interpolation calculations.
    (2)OpenGL: Graphics simulation is developed using this.

    Robustness of solution

    The solution for Direct Kinematic Analysis is robust, and gives a exact task space coordinates. Whereas the inverse kinematic solution is not robust, because the errors in initial 3 joint angles gets added cumulatively from first to third link. Since initial 3 angles are needed for caliculating orientation matrix obviously, this proves to be erraneous. With these results the last 3 wrist angles gets effected. So we conclude that the last three joint angles are more delicate to errors. The occurance of error is random and doesn't follow any function. 

    Future Work

    Annotated Bibliography

    1. Fu KS, Gonzolez & Lee-Robotics (control,sensing and vision), Mc.Graw Hill.
    2. Craig John J - Introduction to Robotics (control and manipulation), Addison-wesley.
    3. Val Programmers Manual, Kawasaki Industries Ltd,.
    4. MatLab (R) Users Giude (V5.2)
    5. simulation of optimal path

    This proposal was prepared by Swaroop and Prasad as a part of the project component in the Course on Computer Aided Engineering Design in the July-December Semester, 1998. (Instructor : Amitabha Mukerjee )

     [CAED COURSE LECTURES HOME PAGE]