AUTOMATIC MESH GENERATION (2-D)
COURSE PROJECT
The power of today's massively parallel supercomputers allow users to slove very large and complicated problems in the applications area. Many of these applications involve complex structures such as aircraft, automobiles, or other mechanical parts, and in most of these cases, the only option the user will have to discretise the domain is with an Automatic Mesh Generator. The solution and visualisation of the Finite Element Problems has received much attention, and as these applications become more complex, the modelling and mesh generation (pre-processing) of these problems becomes more of a crucial step in the simulation process.
An automatic Mesh Generator, as a definition, uses some sort of boundary data alone as an input, and then creates the interior nodes and elements automatically based on this boundary data. Since the mesh generator makes little or no assumption on the structure of the domain, almost any structure can be modelled with these mesh generators. The methods we use are based on Delaunay-Voronoi methods. These methods are probably the most general type of automatic mesh generator and result in high quality meshes in both 2D and 3D. The type of mesh they produce is a Delaunay mesh.
Although many algorithms exist for triangulation in an arbitrary number of space dimensions, only a few have been used on practical problems. In particular, Delaunay Triangulation has proven to be a very useful triangulation technique. Here we outline some of the basic concepts surrounding Delaunay and related triangulations as well as discussing some of the most popular algorithms for constructing these triangulations.
Definition: The Delaunay Triangulation of a point set is defined as the dual of the Voronoi diagram of the set.
Properties of a 2D Delaunay Triangulation:

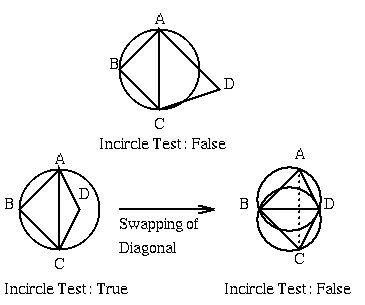
This test is true if the point D lies interior to the circumcircle of triangle ABC. Swapping the edge from position A-C to position B-D gaurentees that the new triangle pair satifies the circumcircle criteria. Furthemore, this process of diagonal swapping is local, i.e. it does not disrupt the Delaunayhood of any triangles adjescent to quadrilateral.
Other properties of Delaunay triangulation are:
These properties are not used directly in the process of triangulation and thus we defer from discussing these here.
ALGORITHMS FOR DELAUNAY TRIANGULATION
We now consider several techniques for Delaunay Triangulation in two dimensions. This is by no means a complete list but all these algorithms work optimally in rather different situations. The dicussion of 2D algorithms is organised as follows:
The algorithm we are using is essentially an Incremental Insertion Algorithm and is based on Green and Sibson Algorithm.