3D Surface Reconstruction from point data 

Objective

To study the method of using Alpha Shapes for 3D surface reconstruction
and look into the 3D scaling aspects on 3D point data set

Motivation

The report is divided in to the following sections :

• Introduction
• Alpha shapes
• 3D Scaling
• Past Work
• Methodology Used
• Distance Metrics Used
• The L one metric
• The L infinity metric
• The Euclidean distance metric
• Results
• Observations
• Conclusion
• References
• [Proposal page for the Project (includes slides of the presentation done)]

Introduction

Alpha Shape

Alpha shapes are a generalization of the convex hull of a point set. It can be used to fit a smooth surface through points in 3D space. The surface may be disjoint. It's a very clean and general method of creating 3D surfaces.

The complete mathematical definition of alpha shapes is quite is quite involved, and is given in [2]. Intuitively we can describe alpha shapes as follows :

Let the point set be S. Think of R³ filled with Styrofoam and the points of S made of more solid material such as rock. Now imagine a spherical eraser with radius alpha. It's omnipresent in the sense that it carves out Styrofoam at all positions where it does not enclose any of the sprinkled rocks, i.e., points of S. The resulting object will be called the alpha hull. To make things more feasible We straighten the surface of the object by substituting straight edges for the circular ones and triangles for spherical caps. The object obtained is the alpha shape of S. It's a polytope in a fairly general sense. It can be concave or even disconnected. It can contain 2D patches of triangles and 1 dimensional strings of edges; and it's components can be as small as single points. The parameter alpha controls the maximum ``curvature '' of any cavity of the polytope.

^{Scaling of 3D Shapes}

The intention is to drop points from the 3D data set, so that the time taken for surface generation is reduced, on the cost of losing some minor details in the surface. But the overall surface generated should resemble the original. For this we have devised different metrics and scaling algorithms which is discussed in the next section.

back to the index

Past Work

Herbert Edelsbrunner & Ernst P. Mucke at NCSA UIUC, have been working extensively on 3D surface generation using alpha shapes. They have provided a rigorous and mathematical definition of alpha shapes in [2]

A research release of the implementatiion of their work is available via ftp at [ftp://ftp.ncsa.uiuc.edu/Visualization/Alpha-shape/alpha-2.2/alpha-2.2.sgi.tar.gz]

back to the index

Methodology Used

Alpha shape generation goes through following stages :

• Delaunay triangulation
The definition of Delaunay triangulation is given in [2]. The alpha visualizer employs a variant of the randomized incremental-flip algorithm due to Edelsbrunner and Shah [3]. The variant and its data structure is described in more detail in Mucke [4].
• Computation of the Alpha interval

Algorithms for Scaling

The distance referred to in this Algorithm is calculated using 3 different metrics. The details of the metrics are given in the next section.

step 1 : Sort the points in S (using Quick Sort) and remove duplicates

step 2 : Calculate the standard deviation of the x coordinates, y coordinates and z coordinates of the points

step 3 : Sort the points with the coordinate with maximum deviation first, the coordinate with second maximum deviation  second and so on

(Now, in the sorted order, if two points are consecutive then they are most likely to be in the same cluster. The heuristic of sorting after finding the standard deviation may be replaced by a better measure of locality)

step 4 : Calculate the threshold as the fraction of the distance between the extreme points

step 5: A window, whose size depends on the number of windows needed, centered around each point is moved from the first point to the last point.

For each point in the window do the following

Find the distance of each point from the center of the window. If this distance is less than the threshold then we add this point to the proximity list of the center of the window. Also find the size of each list and the maximum and minimum size so far.

(Now we have the proximity list for all the points)

step 6: Drop all points with size of proximity list greater than the critical_distance with some probability. ( Note : We take the critical_distance into consideration to retain the sparse points of the surface. The probabilistic dropping is to take care of the other extreme, i.e., all the points belonging to a cluster may be dropped).

We now have a set of points, with cardinality less than that of S, which retains all the ``important'' features of the original, but removes most of the minor details.

As the Delaunay triangulation and subsequent alpha shape generation time are heavily dependent on the cardinality of S, we are saving on time by reducing the cardinality of the point set.

back to the index

Distance Metrics

The L one metric

Distance between (x₁,y₁,z₁) and (x₂,y₂,z₂) is

|(x₁-x₂)| + |(y₁-y₂)| + |(z₁-z₂)|

The L infinity metric

Distance between (x₁,y₁,z₁) and (x₂,y₂,z₂) is

maximum ( |(x₁-x₂)| ,|(y₁-y₂)| ,|(z₁-z₂)| )

The Euclidean distance metric

Distance between (x₁,y₁,z₁) and (x₂,y₂,z₂) is

sqrt ( (x₁-x₂)²+ (y₁-y₂)² + (z₁-z₂)² )

We are using L one and L infinity metric so that we can work with long integer arithmetic. This considerably speeds up the computation.

back to the index

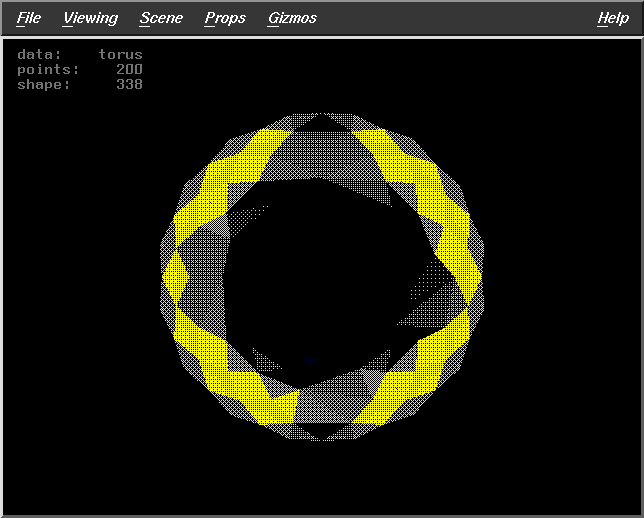
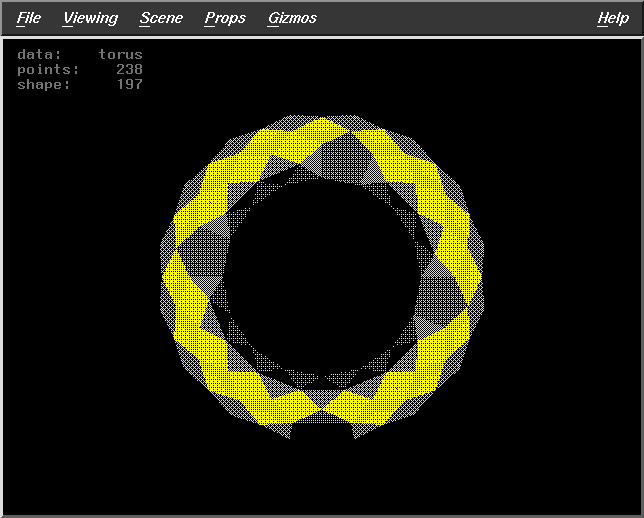
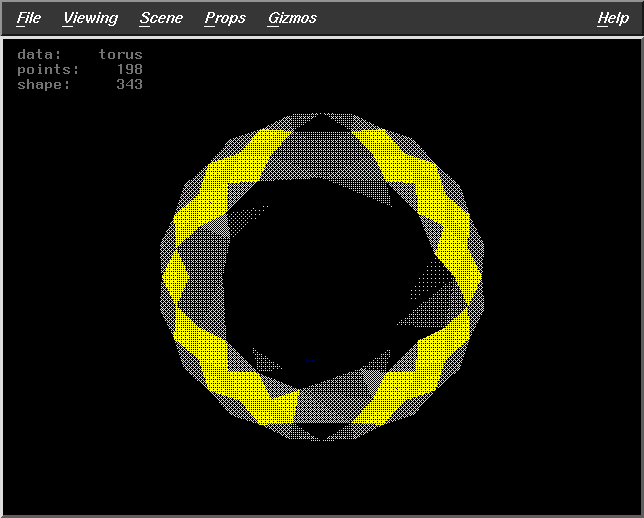
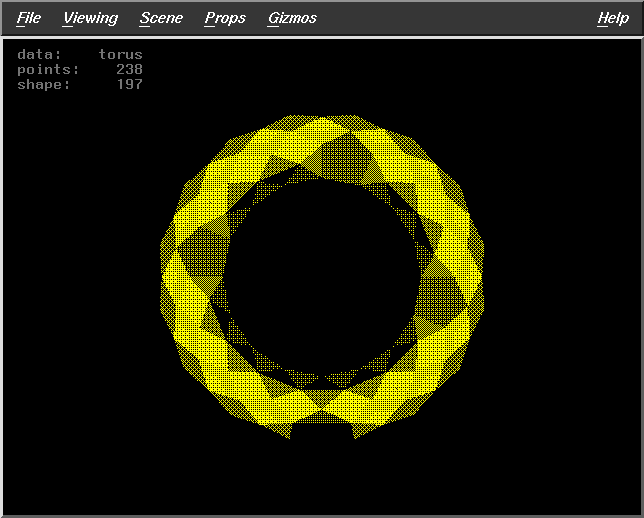
Results

We have implemented these algorithms and incorporated it into the code of the alpha-visualizer. The test runs of the visualizer gave the following results on surface reconstruction of a torus using a point data set of size 256. The parameters that may be varied are :

• Algorithm
• Fraction of the maximum distance to be considered.
• A parameter to govern the window size
• Probability of dropping a selected point, a number ``n'' in the following table implies a probability of 1/n.

The results for the three algorithms are :

Results for Algorithm 1

Fract=0.5      WS=10      DF=2      Pts=200	Fract=0.5      WS=10      DF=7      Pts=238
Fract=0.5      WS= 30      DF=2      Pts=198	Fract=0.5      WS=30      DF=7      Pts=238
Fract=0.8      WS=10      DF=2      Pts=154	Fract=0.8      WS=10      DF=7      Pts=224
Fract=0.8      WS=30      DF=2      Pts=139	Fract=0.8      WS=30      DF=7      Pts=219

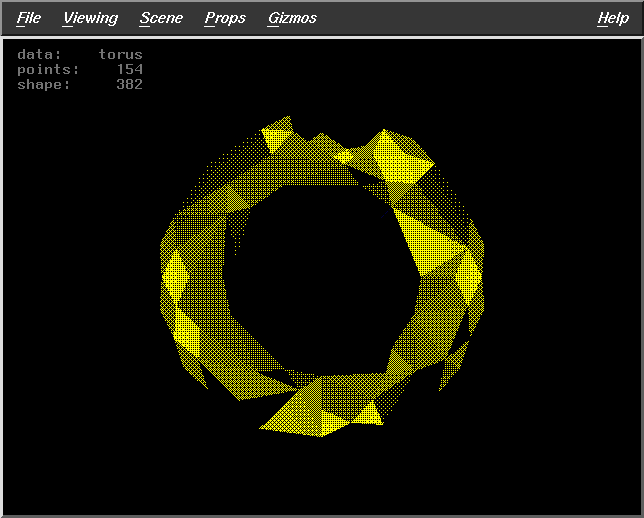
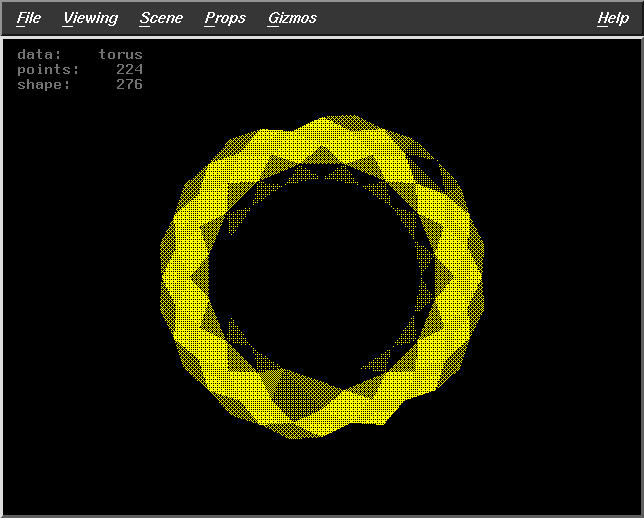
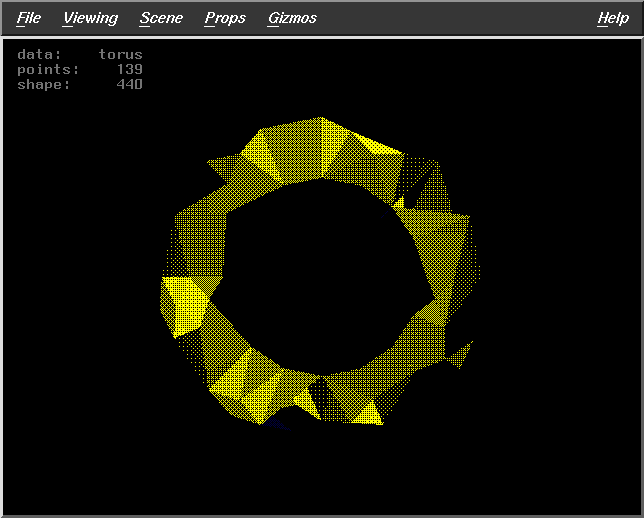
Results for Algorithm 2

Fract=0.5      WS=10      DF=2      Pts=155	Fract=0.5      WS=10      DF=7      Pts=224
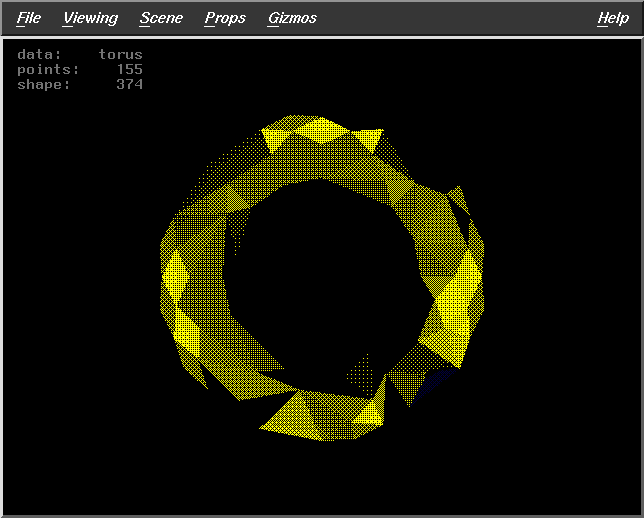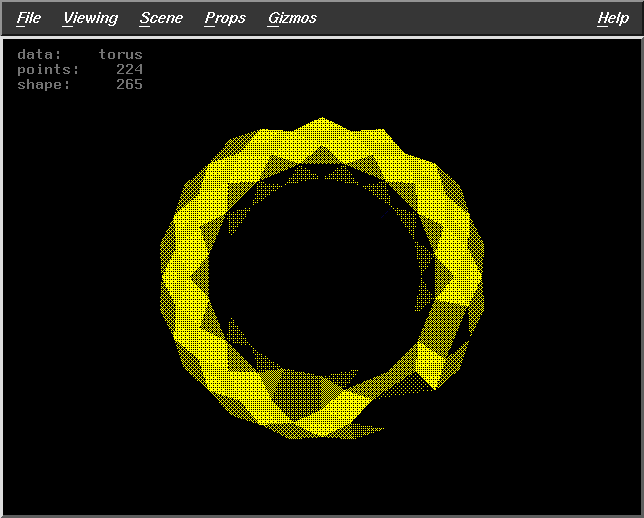Fract=0.5      WS=30      DF=2      Pts=139	Fract=0.5      WS=30      DF=7      Pts=219
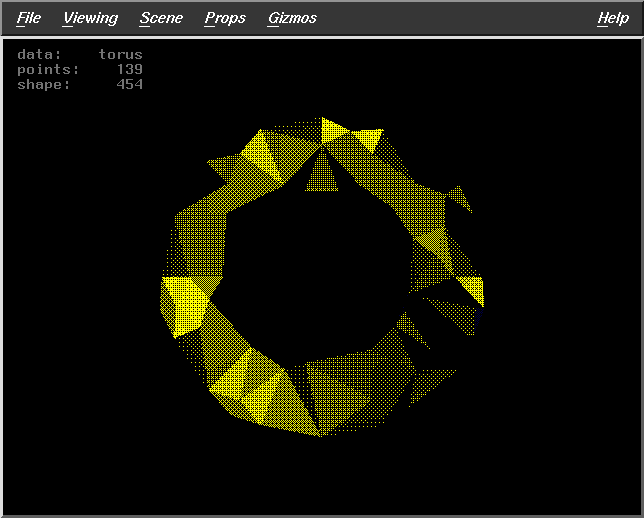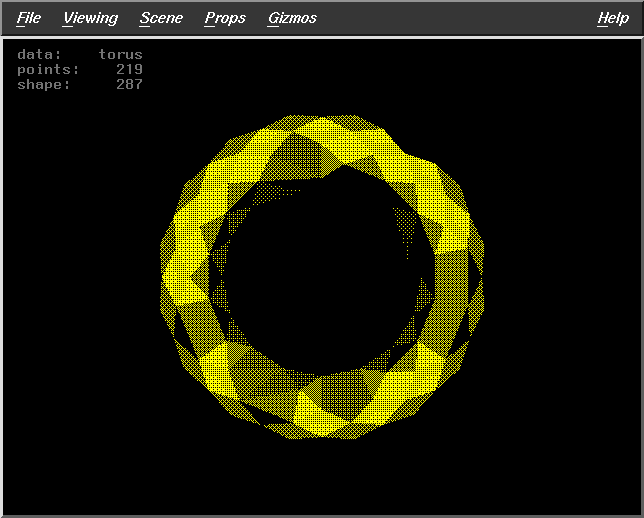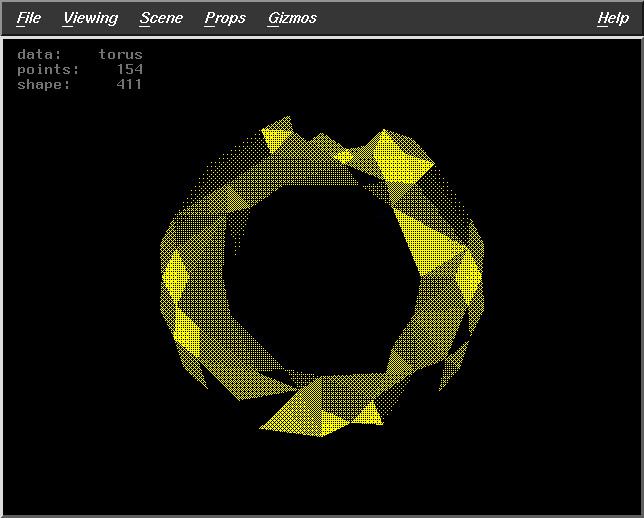
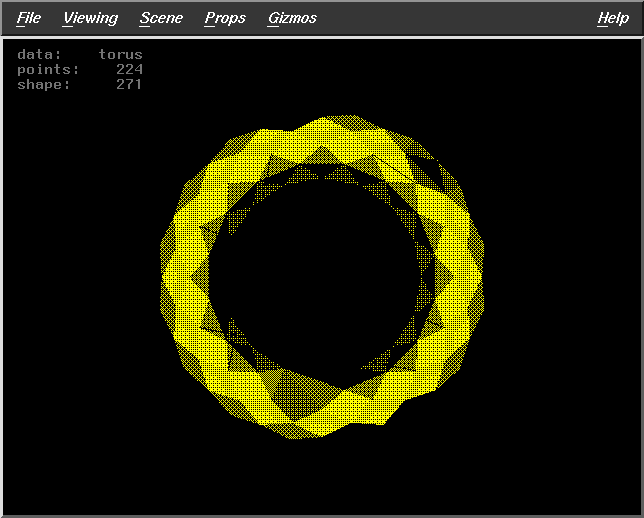
Fract=0.8      WS=10      DF=2      Pts=154	Fract=0.8      WS=10      DF=7      Pts=224
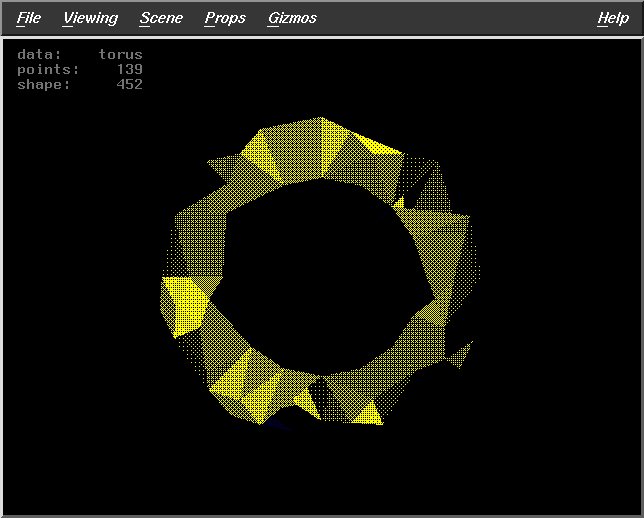
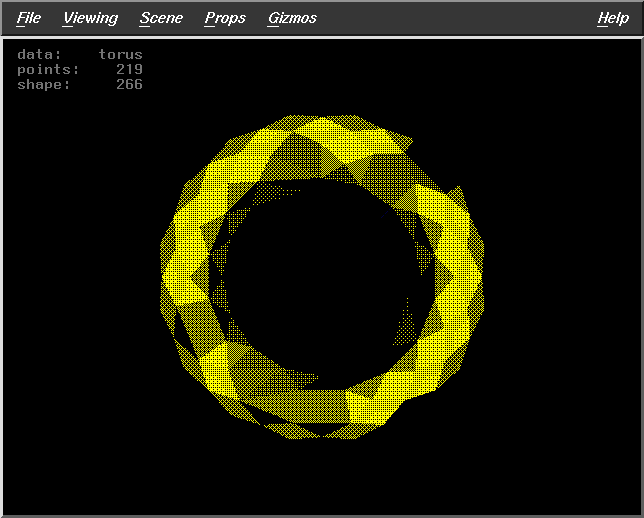
Fract= 0.8      WS=30      DF=2      Pts=139	Fract=0.8      WS=30      DF=7      Pts=219

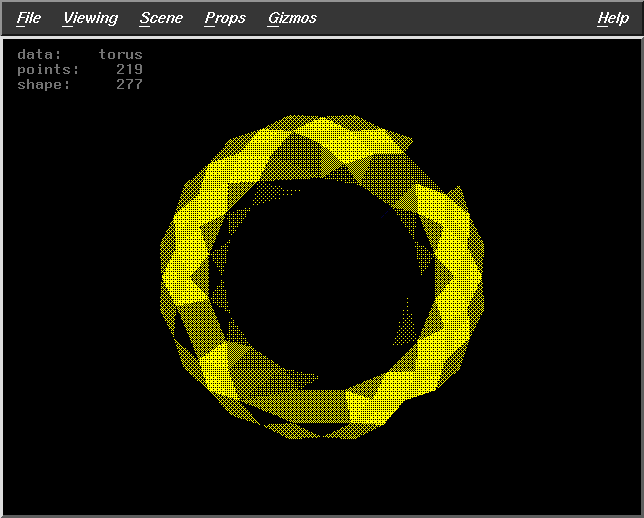
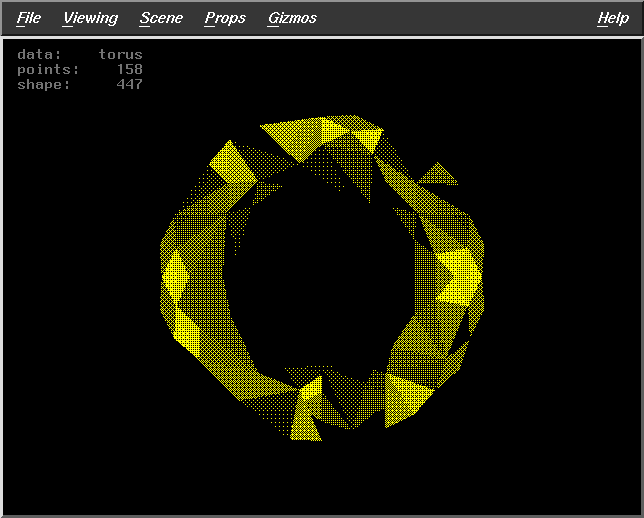
Results for Algorithm 3

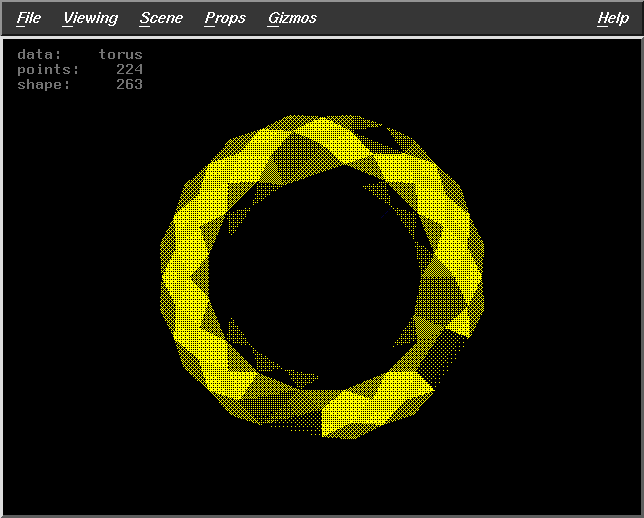
Fract=0.5      WS=10      DF=2      Pts=158	Fract=0.5      WS=10      DF=7      Pts=224
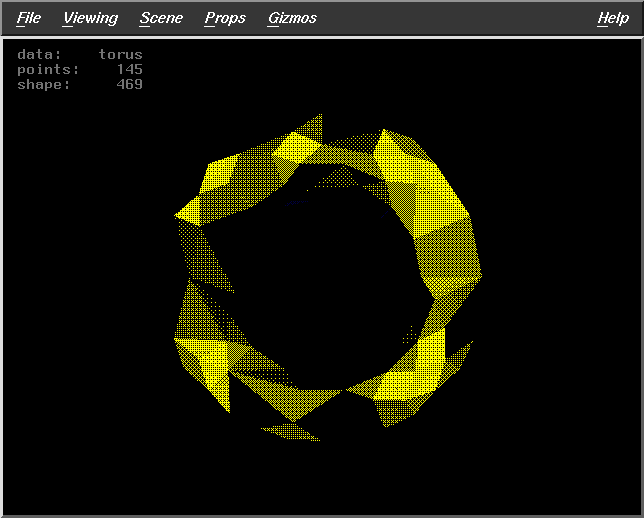
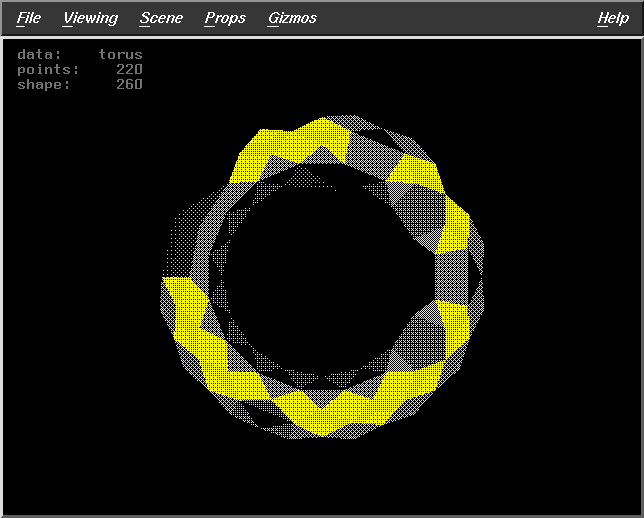
Fract=0.5      WS=30      DF=2      Pts=145	Fract=0.5      WS=30      DF=7      Pts=220
Fract=0.8      WS=10      DF=2      Pts=154	Fract=0.8      WS=10      DF=7      Pts=224
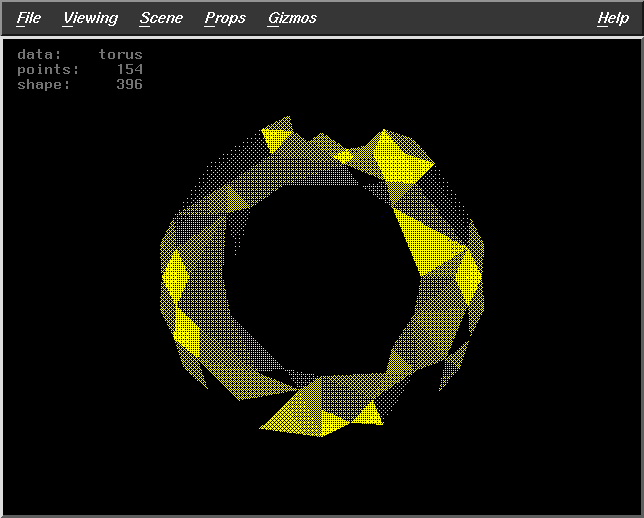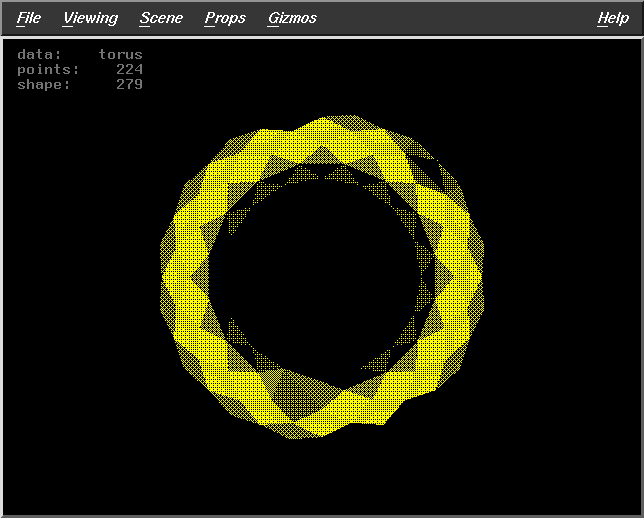Fract=0.8      WS=30      DF=2      Pts=139	Fract=0.8      WS=30      DF=7      Pts=219

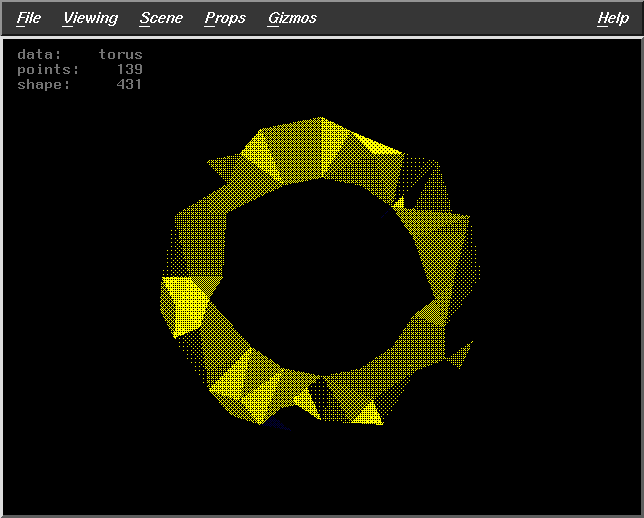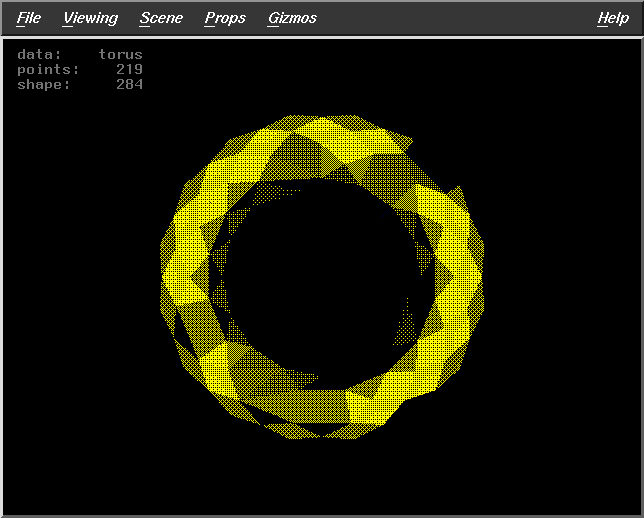back to the index

Observation

From the results tabulated above the following can be inferred :

• By increasing the fraction more number of points are dropped. This is due to the fact that the radius considered for making the clusters is increased.
• By increasing the window scale more number of points are considered for being dropped.
• As expected, increasing the probability of dropping resulted in more no of points being dropped.
• Algorithm 1 drops lesser points as compared to the other two algorithms used.

back to the index

Conclusion

We have devised a new algorithm to reduce the number of points needed for alpha shape generation that retains the important features of the original surface and speeds up the generation of alpha shape at the cost of losing some minor details. The results that we got were quite satisfactory. Improvements can be done to the algorithm by using better metrics to find clusters and dropping probability can also be made dependent on some cluster properties.

back to the index

References

[1] ``Surface Reconstruction : From points to Splines'', Baining Guo, CAD, vol 29, No. 2, 1997

[2] ``Three-Dimensional Alpha Shapes'', Herbert Edelsbrunner, Ernst P. Mucke, ACM Transaction on Graphics, vol 13, No. 1, Jan 1994, p43-72
[ftp://cs.uiuc.edu/pub/edels/geometry/shapes-94.Z]

[3] ``Incremental topological flipping works for regular triangulations. Herbert Edelsbrunner, Nimish Shah, Proceedings of the 8th Annual Symposium on Computational Geometry, 1992, 43-52.

[4] ``Shapes and Implementations in Three-Dimensional Geometry'', Ernst Mucke, Ph.D. Thesis, Department of Computer Science, University of Illinois at Urbana Champaign. Technical Report UIUCDCS-R-93-1836.
[ftp://cs.uiuc.edu/pub/TechReports/UIUCDCS-R-93-1836.ps.Z].

back to the index

This page is maintained by Anoop Jayadevan (anoop@cd1) and Sachin Maheshwari (sach@cd1)